Veri yapıları ve nümerik analize genel bakış
İndeks
- 1. Veri Yapıları
- 1.1. Veri Yapısı Tanımı
- 1.2. Veri Yapısı Gösterimi
- - 1.2.1. Satır Önce Yerleşim
- - 1.2.2. Sütun Önce Yerleşim
- - 1.2.3. Sıra Düzeni İle Yerleşim
- 1.3. Veri Yapısı Denetim Grubuna Erişim
- 1.4. Veri Öğesine Erişim
- 2. Veri Yapısının Gruplandırılması
- - 2.1. Statik Veri Yapıları
- - 2.2. Dinamik Veri Yapıları
- - 2.3. Veri ve Verinin Saklanması
- - 2.4. Verinin İletimi İşlemi
- - 2.5. Veri Yapısı Üzerindeki Operasyonlaar
- - - 2.5.1. Oluşturma (Creation)
- - - 2.5.2. Yok etme (Destroy)
- - - 2.5.3. Seçim (Selection)
- - - 2.5.4. Güncelleme (Update)
- - 2.6. Veri Yapıları İçin Belirlenen İşleem Tipleri
- - - 2.6.1. Diziler (array)
- - - 2.6.2. Liste (list)
- - - 2.6.3. Katar (string)
- - - 2.6.4. Kütük (file)
- - - 2.6.5. Kayıt (record)
- - 2.7. Liste Yapıları
- - - 2.7.1. Kuyruk (Queue)
- - - 2.7.2. Yön (Stack)
- - 2.8. Liste Yapılarının Uygulama Alanlarrı
- - - 2.8.1. Uygulama Alanı
- - - 2.8.2. Uygulama Alanı
- - - 2.8.3. Uygulama Alanı
- - 2.9. Ana Programdan Alt Program Paramettre Aktarma
- - - 2.9.1. Değer Çağırma Yöntemi (Call byy value)
- - - 2.9.2. Adres Çağırma Yöntemi (Call byy adress)
- - - 2.9.3. Sonuç Çağırma Yöntemi (Call byy result)
- - - 2.9.4. Değer Sonuç Çağırma Yöntemi (CCall by value-result)
- - 2.10. Kuyruk Yapısının Uygulama Alanlarrı
- 3. Çizge ve Ağaç Yapısı
- - 3.1. Yönsüz Çizge
- - - 3.1.1. Maliyet Matrisi
- - - 3.1.2. Komşuluk Maliyet Matrisi
- - 3.2. Yönlü Çizge
- - - 3.2.1. Komşuluk Maliyet Matrisi
- - - 3.2.2. Mantıksal Komşuluk ve Maliyet Vektörü
- - - 3.2.3. Komşuluk Maliyet Listeleri
- - - 3.3. Ağaç Veri Yapısı
- - - 3.3.1. İleriye Doğru Bağlaçlı (Forwarrd Linked Tree)
- - - 3.3.2. Geriye Doğru Bağlaçlı (Backwarrd Linked Tree)
- - 3.4. İkili Ağaç Veri Yapısı
- - - 3.4.1. Bağlaçsız Gösterim (düğüm sayıısı sabit)
- - - 3.4.2. Geriye Doğru Bağlaçlanmış İkilli Ağaç Gösterimi
- - - 3.4.3. İleriye Doğru Bağlaçlanmış İkiili Ağaç Gösterimi
- - - 3.4.4. Çift Yönlü Bağlaçlanmış İkili Ağaç Gösterimi
- - 3.5. Sıralama Ağacı (Sort Tree)
- 1.1. Veri Yapısı Tanımı
- 1.2. Veri Yapısı Gösterimi
- - 1.2.1. Satır Önce Yerleşim
- - 1.2.2. Sütun Önce Yerleşim
- - 1.2.3. Sıra Düzeni İle Yerleşim
- 1.3. Veri Yapısı Denetim Grubuna Erişim
- 1.4. Veri Öğesine Erişim
- 2. Veri Yapısının Gruplandırılması
- - 2.1. Statik Veri Yapıları
- - 2.2. Dinamik Veri Yapıları
- - 2.3. Veri ve Verinin Saklanması
- - 2.4. Verinin İletimi İşlemi
- - 2.5. Veri Yapısı Üzerindeki Operasyonlaar
- - - 2.5.1. Oluşturma (Creation)
- - - 2.5.2. Yok etme (Destroy)
- - - 2.5.3. Seçim (Selection)
- - - 2.5.4. Güncelleme (Update)
- - 2.6. Veri Yapıları İçin Belirlenen İşleem Tipleri
- - - 2.6.1. Diziler (array)
- - - 2.6.2. Liste (list)
- - - 2.6.3. Katar (string)
- - - 2.6.4. Kütük (file)
- - - 2.6.5. Kayıt (record)
- - 2.7. Liste Yapıları
- - - 2.7.1. Kuyruk (Queue)
- - - 2.7.2. Yön (Stack)
- - 2.8. Liste Yapılarının Uygulama Alanlarrı
- - - 2.8.1. Uygulama Alanı
- - - 2.8.2. Uygulama Alanı
- - - 2.8.3. Uygulama Alanı
- - 2.9. Ana Programdan Alt Program Paramettre Aktarma
- - - 2.9.1. Değer Çağırma Yöntemi (Call byy value)
- - - 2.9.2. Adres Çağırma Yöntemi (Call byy adress)
- - - 2.9.3. Sonuç Çağırma Yöntemi (Call byy result)
- - - 2.9.4. Değer Sonuç Çağırma Yöntemi (CCall by value-result)
- - 2.10. Kuyruk Yapısının Uygulama Alanlarrı
- 3. Çizge ve Ağaç Yapısı
- - 3.1. Yönsüz Çizge
- - - 3.1.1. Maliyet Matrisi
- - - 3.1.2. Komşuluk Maliyet Matrisi
- - 3.2. Yönlü Çizge
- - - 3.2.1. Komşuluk Maliyet Matrisi
- - - 3.2.2. Mantıksal Komşuluk ve Maliyet Vektörü
- - - 3.2.3. Komşuluk Maliyet Listeleri
- - - 3.3. Ağaç Veri Yapısı
- - - 3.3.1. İleriye Doğru Bağlaçlı (Forwarrd Linked Tree)
- - - 3.3.2. Geriye Doğru Bağlaçlı (Backwarrd Linked Tree)
- - 3.4. İkili Ağaç Veri Yapısı
- - - 3.4.1. Bağlaçsız Gösterim (düğüm sayıısı sabit)
- - - 3.4.2. Geriye Doğru Bağlaçlanmış İkilli Ağaç Gösterimi
- - - 3.4.3. İleriye Doğru Bağlaçlanmış İkiili Ağaç Gösterimi
- - - 3.4.4. Çift Yönlü Bağlaçlanmış İkili Ağaç Gösterimi
- - 3.5. Sıralama Ağacı (Sort Tree)
İÇERİK
1. Veri Yapıları
Veri veri tabanına kayıtlı fiziksel değerlerdir. verinin işlenmiş hali ise bilgidir
Veri Yapısı düzenli bir veri maddeleri kümesidir.
Veri Tabanı birbiriyle ilişkili veriler topluluğudur. veri tabanı sadece veriye değil veriler arasındaki ilişkiyi de saklar.
Algoritma bir problemi sistematik olarak adım adım çözmek için kullanılan yöntemdir. bir algoritmanın varlığından söz edebilmek için algoritmanın sunduğu kurallar kümesi hiçbir şüpheye yer vermeyecek kadar kesin olması lazım ve algoritmanın duracağı bir nokta kesin olarak belirtilmelidir.
Veri veri tabanına kayıtlı fiziksel değerlerdir. verinin işlenmiş hali ise bilgidir
Veri Yapısı düzenli bir veri maddeleri kümesidir.
Veri Tabanı birbiriyle ilişkili veriler topluluğudur. veri tabanı sadece veriye değil veriler arasındaki ilişkiyi de saklar.
Algoritma bir problemi sistematik olarak adım adım çözmek için kullanılan yöntemdir. bir algoritmanın varlığından söz edebilmek için algoritmanın sunduğu kurallar kümesi hiçbir şüpheye yer vermeyecek kadar kesin olması lazım ve algoritmanın duracağı bir nokta kesin olarak belirtilmelidir.
Veri yapısının incelenmesi
Bir veri yapısı incelenirken şu adımlardan geçerek belirleme hem açıklık sağlayacak hemde güvenilir program yazmaya yöneltecektir.
Bir veri yapısı incelenirken şu adımlardan geçerek belirleme hem açıklık sağlayacak hemde güvenilir program yazmaya yöneltecektir.
1.1. Veri Yapısı Tanımı
1.2. Veri Yapısı Gösterimi
1.3. Veri Yapısı Denetim Grubuna Erişim
1.4. Veri Öğesine Erişim
1.2. Veri Yapısı Gösterimi
1.3. Veri Yapısı Denetim Grubuna Erişim
1.4. Veri Öğesine Erişim
Bu belirtilen adımlar, önemli olan ve sık kullanılan veri yapısı için incelenmelidir. bu kavramları dizi, matris gibi bilinen veri yapısı üzerinde uygulayalım.
1.1. Veri Yapısı Tanımı veri yapısının zorunlu başlangıç değerleri ve geçerlilik göstergeleri (varsa) bu düzeyde tanımlanır.
Örnek A(0:2, -1:+1) dizisini tanımlamamız gerektiğinde şekilde görüldüğü gibi bir matris olarak tanımlanır.
A | -1 | 0 | +1 |
| 0 | |||
| 1 | |||
| 2 |
1.2. Veri Yapısı Gösterimi veri yapısının bilgisayar belleğine yerleşim biçimidir. kullanılan bilgisayarın bellek sözcük boyutu dikkate alınarak bellekte uygun bir yerleşim düzenlenir.
1.2.1. Satır Önce Yerleşim
| A(0, -1) | |
| A(0, 0) | |
| A(0, +1) | |
| A(1, -1) | |
| A(1, 0) | |
| A(1, +1) | |
| A(2, -1) | |
| A(2, 0) | |
| A(2, +1) |
1.2.2. Sütun Önce Yerleşim
| A(0, -1) | |
| A(1, -1) | |
| A(2, -1) | |
| A(0, 0) | |
| A(1, 0) | |
| A(2, 0) | |
| A(0, +1) | |
| A(1, +1) | |
| A(2, +1) |
1.2.3. Sıra Düzeni İle Yerleşim
1.3. Veri Yapısı Denetim Grubuna Erişim Belleğin bir bölgesinde yerleştirilmiş olan veri yapısı gösterimi başlangıcına erişimdir. yani veri yapısının sembolik adı ile bellekteki yerleşim adresinin eşleştirilmesidir.
Örnek
Adres (A)
Adres (A)
|
-->
| Bellek
|
1.4. Veri Öğesine Erişim Veri yapısı denetim grubundan geçerken geçerliliğin sağlanması yazılım güvenirliliği çok önemlidir. Dizi veri yapısını kullanan birçok programlama dili işletim etkinliğini kaybetmemek için bu noktayı göz ardı ederler. Bir veri öğesine erişim geçerli değilse ve bu durum Veri Yapısı Denetim Grubunda incelenerek bulunabiliyorsa bu yanlış erişim hemen ve açıklıkla belirterek erişimi engelleyecek program kesimleri yazılmalıdır.
2. Veri Yapısının Gruplandırılması Veri yapıları statik ve dinamik olmak üzere ikiye ayrılır.
2.1. Statik Veri Yapıları Program yazılırken tam olarak belirlenen ve program tarafından değiştirilemeyen veri yapılarıdır. Örnek diziler, kayıt yapıları.
2.2. Dinamik Veri Yapıları Program tarafından yapısı değiştirilen veri yapısıdır. Örnek dosya veya dosyalar tarafından eleman yada kayıt yapısı sayı değiştirilebildiği için dinamik veri yapısıdır.
2.3. Veri ve Verinin Saklanması Veri yapılarını incelerken verinin verinin ne anlama geldiğinin, nasıl iletildiğini ve nasıl saklandığını incelemek gerekir. Bilgisayar bilimi tamamıyla veriye erişim, verinin işlenmesi ve depolanmasıyla ilgilenir.
2.4. Verinin İletimi İşlemi Verinin İletimi İşlemi 5 elemandan oluşan bir sistem olarak incelenir
2.4. Verinin İletimi İşlemi Verinin İletimi İşlemi 5 elemandan oluşan bir sistem olarak incelenir
1) Kaynak (Mesaj jenaratörü)
2) Çevirici (Kodlayıcı, Encoder)
3) Kanal (Nakledici)
4) Algılayıcı (Decoder)
5) Hedef (Alıcı)
2) Çevirici (Kodlayıcı, Encoder)
3) Kanal (Nakledici)
4) Algılayıcı (Decoder)
5) Hedef (Alıcı)
| Tetikleme | Kaynak | Mesaj | Çevirici | Gönderilen | Kanal | -> | Algılayıcı | Gönderilen (msj) | Hedef | Tepki |
Verinin Saklanması sayısal bilgisayarlarda iki tip bellek ünitesi vardır. Bunlar register denilen işlemsel üniteler ve depolama (RAM, Disk) üniteleridir. Bir register bilgiyi işleme ve geçici olarak saklamak için kullanılır. CPU içinde bulunur.
2.5. Veri Yapısı Üzerindeki Operasyonlar
2.5. Veri Yapısı Üzerindeki Operasyonlar
2.5.1. Oluşturma (Creation) Veri yapılarıyla ilgili olarak en sık yapılan işlem yeni bir veri yapısı oluşturmaktır. Bu işlem bir değişken tanımlayıp bu değişkene karşılık gelecek veri için bellekte yer ayırmakla olur.
2.5.2. Yok etme (Destroy) Veri yapısını iptal etmek için kullanılır. Veri yapısının ilgili kısmı yada tamamı silinir.
2.5.3. Seçim (Selection) En sık kullanılan operasyondur. Veri yapısı içindeki bir veriye erişmektir.
2.5.4. Güncelleme (Update) Veri yapısındaki bir veriyi güncellemektir. Yani değiştirmektir.
2.6. Veri Yapıları İçin Belirlenen İşlem Tipleri Veri yapılarında kullanılan işlem tipleri 5 tanedir.
2.6.1. Diziler (array) Veri maddelerinin bir veya çok boyutlu olarak düzenlenmiş halidir ve dizinin en belirgin özelli aynı tip elemanlardan oluşması ve eleman sayısının sınırlı oluşudur. Diziler üzerinde yapılabilecek işlemler.
a) Veri maddelerini okumak
b) Toplam ve ortalama değerlerini okumak
c) Ortalamanın altında ve üstünde olan veri madde sayısını bulmak
d) En büyük ve en küçük veri maddelerini saptamak
e) Arama yapmak
f) Sıralamak
g) Elemanların yerini değiştirmek
h) Dizileri birleştirmek
b) Toplam ve ortalama değerlerini okumak
c) Ortalamanın altında ve üstünde olan veri madde sayısını bulmak
d) En büyük ve en küçük veri maddelerini saptamak
e) Arama yapmak
f) Sıralamak
g) Elemanların yerini değiştirmek
h) Dizileri birleştirmek
2.6.2. Liste (list) Değişken sayıda eleman içeren düzenli bir veri grubudur. Listede silme ve araya ekleme yapılabilir. Liste üzerinde yapılabilecek işlemler
a) Listenin uzunluğu ve eleman sayısını saptamak
b) Listede belli bir elemanı aramak
c) Listenin kopyasını çıartmak
d) Listenin elemanlarını sınıflamak
e) İki veya daha çok listeyi birleştirmek
f) Bir listeyi alt listelere ayırmak
b) Listede belli bir elemanı aramak
c) Listenin kopyasını çıartmak
d) Listenin elemanlarını sınıflamak
e) İki veya daha çok listeyi birleştirmek
f) Bir listeyi alt listelere ayırmak
2.6.3. Katar (string) Karakterlerden (Nümerik, Alfa nümerik, Spesiyal) oluşan bir dizi bilgidir. Katarlar üzerinde yapılabilecek işlemler
a) Bir yazı oluşturmak
b) İki katarı birleştirmek
c) Arama yapmak
d) Alt katarı ana katara eklemek
e) İki katarın eşitliğini sınamak (büyüklük, küçüklük ve eşitlik)
f) Katar uzunluğu hesaplamak
g) Alt katarlar oluşturmak
h) Katarlat içinde alt katarlar aramak
b) İki katarı birleştirmek
c) Arama yapmak
d) Alt katarı ana katara eklemek
e) İki katarın eşitliğini sınamak (büyüklük, küçüklük ve eşitlik)
f) Katar uzunluğu hesaplamak
g) Alt katarlar oluşturmak
h) Katarlat içinde alt katarlar aramak
2.6.4. Kütük (file) Tipik olarak bilgisayarın dış belleğinde saklanan büyük bir listedir. Belli bir amaçla bir araya getirilen kayıt topluluğudur. Dış bellekte ana belleğin aksine farklı liste parçalarına erişmek için gereken bilgi düzenlenmesi veya organizasyonu ve zaman eşit değildir.
2.6.5. Kayıt (record) Birbiriyle ilişkili veri maddelerinden oluşan bir boyutlu dizilere benzer ancak dizideki elemanları aynı tipte olduğu halde kayıttaki elemanları farklı tipte olabilir.
2.7. Liste Yapıları İki tür listeye erişim vardır.
2.7. Liste Yapıları İki tür listeye erişim vardır.
2.7.1. Kuyruk (Queue) Bir ucuna yeni eleman eklemeyi diğer ucundan eleman çıkartmayı sağlayan listelerdir. Burada ardışık olarak gelen elemanlara FIFO (First In First Out) (İlk Giren İlk Çıkar) kuralı uygulanır.
2.7.2. Yön (Stack) Sadece ucundan ekleme veya çıkartma yapılabilen listelerdir. Burada ardışık olarak gelen elemanlara LIFO (Last In First Out) (Son Giren İlk Çıkar) kuralı uygulanır.
2.8. Liste Yapılarının Uygulama Alanları
2.8.1. Uygulama Alanı Recursion İşlemi Bir işlemi kendisi vasıtasıyla tanımlama tekniğine denir. Kendi kendini çağırabilen fonksiyolara recursion fonksiyon denilir. Recursion işleminin sağlaması gereken iki işlevi vardır.
- fonksiyonun kendi kendini çağırması.
- işlemi veya hesaplamanın durması için bir koşul olması.
- fonksiyonun kendi kendini çağırması.
- işlemi veya hesaplamanın durması için bir koşul olması.
2.8.2. Uygulama Alanı Stack makinalarında 3 grup komut vardır.
- Grup ekleme komutu (push)
- Grup alma komutu (pop)
- Temel matematiksel işlemler (add, sub, mul, div)
- Grup ekleme komutu (push)
- Grup alma komutu (pop)
- Temel matematiksel işlemler (add, sub, mul, div)
2.8.3. Uygulama Alanı Aritmetik ifadelerin bizim kullandığımız matematik notasyonlarından başka iki çeşit notasyonlarda daha vardır.
a) Polish notasyonu
1) Suffix (operator operanttan sonra yazılır)
2) Prefix (operant operatorden sonra yazılır)
b) Infix notasyonu
a) Polish notasyonu
1) Suffix (operator operanttan sonra yazılır)
2) Prefix (operant operatorden sonra yazılır)
b) Infix notasyonu
| Operant | Operator | Operant |
| a | + | b |
Örnek
| Infix | Suffix | Prefix |
| a | a | a |
| a+b | ab+ | ++abc |
| a+b+c | ab+c+ | ++abc |
| a+(b+c) | abc++ | +a+bc |
| a+b*c | abc*+ | +a*bc |
| a*(b+c) | abc+* | *a+bc |
| a*b*c | ab*c* | **abc |
2.9. Ana Programdan Alt Program Parametre Aktarma
| Program ana Begin . . P=A1 ( ) . . End | Program A1 Begin . . Q=A2 ( ) . . End | Program A2 Begin . . R=A3 ( ) . . End | Program A3 Begin . . . . . End |
Parametre Aktarma Yöntemleri
2.9.1. Değer Çağırma Yöntemi (Call by value) Gerçek parametre adresindeki veri, formal parametre adresindeki veriye aktarılacağı için hem cağrılan program hem de çağıran program aynı veriye erişebilir.
2.9.1. Değer Çağırma Yöntemi (Call by value) Gerçek parametre adresindeki veri, formal parametre adresindeki veriye aktarılacağı için hem cağrılan program hem de çağıran program aynı veriye erişebilir.
2.9.2. Adres Çağırma Yöntemi (Call by adress) Burada da gerçek parametrelerin bellek hücresindeki adres, adres çağırma işlemine aktarılır. Bu yöntemlerde hem çağıran hem de çağrılan alt program aynı veriye erişebilir.
2.9.3. Sonuç Çağırma Yöntemi (Call by result) Alt program çağrıldığında formal parametreye başlangıç değeri verilmez. Gerçek değer alt programdan ana programa aktarır.
2.9.4. Değer Sonuç Çağırma Yöntemi (Call by value-result) Girdi çıktı parametrelerine aktarmak için kullanılır. Gerçek değer, değer çağırmadaki gibi ana programdan alt programa aktarılır. Sonuç çağırmadaki gibi alt programdan ana programa aktarılır.
2.10. Kuyruk Yapısının Uygulama Alanları Kuyruk yapısı en çok benzetme (simülasyonda) kullanılır. İşletmecilik, sosyal bilimler, inşaat ve ulaşım gibi işlerde kullanılabilir. Simülasyon yapılacak sistem ayrık veya sürekli sistem olmalıdır.
Örnek bir şirketin ekonomi politikasını belirlemek için bu sistemin mali işlerini sistem şeklinde belirlemek ve gelecekteki durumunu belirlemek için kullanılır. Bir simülasyon başında bir takım kabuller aranır.
Örnek bir şirketin ekonomi politikasını belirlemek için bu sistemin mali işlerini sistem şeklinde belirlemek ve gelecekteki durumunu belirlemek için kullanılır. Bir simülasyon başında bir takım kabuller aranır.
3. Çizge Veri Yapısı Bilgisayar alanında en çok kullanılan veri yapıları yönsüz çizge, yönlü çizge, ağaç, ikili ağaç veri yapılarıdır.
3.1. Yönsüz Çizge çizge yapısı hem günlük yaşantımızda hem de iş yönetimi mühendislik ve benzeri dalların uygulanmasında sıkça kullanılan bir yapıdır
Örnek Türkiye'de bazı illeri karayolu bağlantıları ile yolun uzunluğunu gösteren bir şekil çizimi.
Şekilde görünen çizgede iki il arasında yollara kenar iki kenarın (edge) birleştiği yere düğüm (vertex) denilir.
Herhangi bir düğümü küçük harf ve o düğümün indisi ile gösterilir. Çizgeyi oluşturan düğümlerin sırası önemli olmaksızın yalnız bir kere yazıldığı küme V ile gösterilir.
v1 = İstanbul
v2 = İzmir
v3 = Ankara
v4 = Antalya
v5 = Adana
v6 = Samsun
v7 = Erzurum
V(G) = { v1, v2, v3, v4, v5, v6, v7 }
Herhangi bir düğümü küçük harf ve o düğümün indisi ile gösterilir. Çizgeyi oluşturan düğümlerin sırası önemli olmaksızın yalnız bir kere yazıldığı küme V ile gösterilir.
v1 = İstanbul
v2 = İzmir
v3 = Ankara
v4 = Antalya
v5 = Adana
v6 = Samsun
v7 = Erzurum
V(G) = { v1, v2, v3, v4, v5, v6, v7 }
Kenarları içinde her kenarı için e, bunların oluşturduğu indisede E denir. Eğer kenarlar üzerinde bir yön çizgisi belirtilmemişse bu tür çizgelere yönsüz çizge denir.
Yönsüz çizgenin kenarları bir parantez şekli içinde o kenarın birleştiği düğümleri yazarak belirtilir (v3, v6) kenarı Ankara, Samsun arasındaki yolu belirtmektedir.
E = { (v1, v2, 507), (v1, v3, 485), (v2, v3, 583), (v2, v4, 515), (v3, v5, 486), (v3, v7, 813), (v4, v5, 500), (v6, v7, 615) }
Bu ilişkiler bilgisayar belleğinde iki şekilde gösterilebilir.
3.1.1. Maliyet Matrisi Matris simetrik olduğundan bir üst üçgensel veya alt üçgensel matris olarak yerleştirilir.
3.1.1. Maliyet Matrisi Matris simetrik olduğundan bir üst üçgensel veya alt üçgensel matris olarak yerleştirilir.
Düğüm adı
| 1 | İstanbul |
| 2 | İzmir |
| 3 | Ankara |
| 4 | Antalya |
| 5 | Adana |
| 6 | Samsun |
| 7 | Erzurum |
Üst üçgensel matris
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 0 | 507 | 485 | 0 | 0 | 0 | 0 |
| 2 | 0 | 583 | 515 | 0 | 0 | 0 | |
| 3 | 0 | 0 | 486 | 418 | 813 | ||
| 4 | 0 | 500 | 0 | 0 | |||
| 5 | 0 | 0 | 0 | ||||
| 6 | 0 | 615 | |||||
| 7 | 0 |
3.1.2. Komşuluk Maliyet Matrisi
Her kenarının iki kez yer aldığı komşuluk maliyet matrisi listeleri yöntemidir.
3.2. Yönlü Çizge
Gerçek uygulamalarda daha çok kullanılan çizge yapısıdır. Yönlü çizge 2 düğüm arasındaki bağlantının yön bilgisini de taşımasıdır. Bu yapıda kenarlar köşeli parantez içinde belirtilir.
V(G) = { 1, 2, 3, 4 }
| 1 | Yeşilköy |
| 2 | Esenboğa |
| 3 | Ercan |
| 4 | Çiğli |
E(6) = { <1, 2: 50>, <1, 4: 60>, <2, 1: 40>, <2, 3: 80>, <2, 4: 70>, <3, 1: 100>, <4, 1:60>, <4, 2:70> }
Örnekte yönlü çizgede Yeşilköy-Esenboğa uçuşunun her iki yönde olduğunu ve 50 dakika sürdüğünü, Esenboğa-Ercan 80 dakikalık tek yönlü bağlantısını ve diğer bağlantıları göstermektedir.
Yönlü Çizgenin Gösterim Şekilleri
Bellek için 3 tane gösterim şekli vardır.
Bellek için 3 tane gösterim şekli vardır.
3.2.1. Komşuluk Maliyet Matrisi
|
|
3.2.2. Mantıksal Komşuluk ve Maliyet Vektörü
|
|
|
Örnekte yönlü çizgede n adet düğüm ve t adet kenar vardır.
3.2.3. Komşuluk Maliyet Listeleri

Yönlü çizgede bazı çözümlemenin yapılması için her düğüm için gelen kenar sayısı belirlenir.

Yönlü çizgede bazı çözümlemenin yapılması için her düğüm için gelen kenar sayısı belirlenir.
| Düğüm | Gelen | Giden | |
| Yeşilköy | 1 | 3 | 2 |
| Esenboğa | 2 | 2 | 3 |
| Ercan | 3 | 1 | 1 |
| Çiğli | 4 | 2 | 2 |
3.3. Ağaç Veri Yapısı
Ağaç yapısı hiyerarşik yapısı nedeniyle programlama ve genel kullanıma çok uygundur. Yapı içerisinde bağlantılar ve bu bağlantıların aitlikleri vardır. Bir ağaç veri yapısı şu şekilde tanımlanmaktadır.
Bir ağaç yapısından söz edebilmek için şu şartlar gerekir
- Bir kök düğüm ile başlanmak zorundadır
- Sadece kökten artarak düğümler çoğalabilirr
- Ağaç yapısı yönsüz çizgedir
- Sadece kökten artarak düğümler çoğalabilirr
- Ağaç yapısı yönsüz çizgedir
Kök Ağacın başlangıç noktasıdır, Örnekte A ağacın köküdür
Düğüm Örnekte kırmızı nokta ile gösterilen bağlanma noktalarına düğüm denilir.
Derinlik Ağacın katman sayısıdır, Örnekte ağacın derinliği 4 tür.
A birinci katman
B ve C ikinci katman
D, E, F, G, H 3. katmandadır.
Ağacın derecesi 3’tür (katmanları toplamı)
Düğüm Örnekte kırmızı nokta ile gösterilen bağlanma noktalarına düğüm denilir.
Derinlik Ağacın katman sayısıdır, Örnekte ağacın derinliği 4 tür.
A birinci katman
B ve C ikinci katman
D, E, F, G, H 3. katmandadır.
Ağacın derecesi 3’tür (katmanları toplamı)
Derece Düğümün alt düğümlerinde bulunan en çok elemanı sayısıdır, örnekte
B’nin derecesi 3’tür (D, E, F)
C’nin derecesi 2’dir (G, H)
Ağacın derecesi 4 tür (en çok elemanı olan katman)
C’nin derecesi 2’dir (G, H)
Ağacın derecesi 4 tür (en çok elemanı olan katman)
Ağacın düğümleri arasındaki ilişkiler
Oğul A nın oğlu B dir
Baba D E F nin babası B dir
Ata H nin ataları C, A dır
Varis B nin varisleri D E F I J K L dir
Oğul A nın oğlu B dir
Baba D E F nin babası B dir
Ata H nin ataları C, A dır
Varis B nin varisleri D E F I J K L dir
Ağaç yapısının bilgisayarda iki şekilde saklayabiliriz
3.3.1. İleriye Doğru Bağlaçlı (Forward Linked Tree) Bellekte çok yer kaplar, kullanımı basittir
- Tüm elemanlar yazıldıktan sonra her birine bir sıra numarası verilir. Bu aynı zamanda elamanın adresidir
- Matrisin sütun sayısı ağacın derecesi kadardır (H en büyük dereceyle ağacın derecesidir ve 4 tür)
- Bağlantı olmayan elamanları düğümlerine 0 yazılır
- Matrisin sütun sayısı ağacın derecesi kadardır (H en büyük dereceyle ağacın derecesidir ve 4 tür)
- Bağlantı olmayan elamanları düğümlerine 0 yazılır
| 1 | A* | 2 | 7 | 0 | 0 |
| 2 | B | 11 | 6 | 1 | 0 |
| 3 | C | 8 | 3 | 0 | 0 |
| 4 | D | 12 | 0 | 0 | 0 |
| 5 | E | 10 | 14 | 0 | 0 |
| 6 | F | 8 | 3 | 0 | 0 |
| 7 | G | 9 | 5 | 0 | 0 |
| 8 | H | 18 | 16 | 15 | 17 |
| 9 | I | 0 | 0 | 0 | 0 |
| 10 | J | 0 | 0 | 0 | 0 |
| 11 | K | 0 | 0 | 0 | 0 |
| 12 | L | 0 | 0 | 0 | 0 |
| 13 | M | 0 | 0 | 0 | 0 |
| 14 | N | 0 | 0 | 0 | 0 |
| 15 | O | 0 | 0 | 0 | 0 |
| 16 | P | 0 | 0 | 0 | 0 |
| 17 | Q | 0 | 0 | 0 | 0 |
| 18 | R | 0 | 0 | 0 | 0 |
Uç dizi
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
Son katmanda kalan elemanların adresleri yazılır (oğulları olmayan elemanlar)
Kök düğümler * ile işaretlenirler.
3.3.2. Geriye Doğru Bağlaçlı (Backward Linked Tree)
Bellekte az yer kaplar, kullanımı karmaşıktır.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A* | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R |
| 0 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 6 | 7 | 7 | 8 | 8 | 8 | 8 |
Her düğümün babasına olan sıra (adres) numarasını saklar. A kök düğüm için 0 yazılır, çünkü bir babası yoktur.
3.4. İkili Ağaç Veri Yapısı
- İkili ağaç veri yapısı kavramsal ttanım düzeyinde bellek içi gösterimden bağımsız olarak şöyle gösterilebilir.
- İkili ağaç veri yapısı iki nokta haricinde ağaç veri yapısı ile aynı özellikleri gösterir.
1. Ağacın derecesi 2 dir.
2. Sol ve sağ alt ağacın yer değiştirilmesi ile çizilen aynı ağaç değildir.
Ağaç Veri Yapısı Gösterimi Bu yöntemler her bir düğümün gösterimi için en az bellek gerektirenden en çok bellek gerektirene doğru sıralanmıştır.
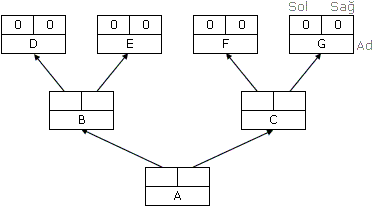
3.4.1. Bağlaçsız Gösterim (düğüm sayısı sabit)
| 1 | A |  |
| 2 | B | |
| 3 | C | |
| 4 | D | |
| 5 | E | |
| 6 | F | |
| 7 | G |
3.4.2. Geriye Doğru Bağlaçlanmış İkili Ağaç Gösterimi
3.4.3. İleriye Doğru Bağlaçlanmış İkili Ağaç Gösterimi
3.4.4. Çift Yönlü Bağlaçlanmış İkili Ağaç Gösterimi
3.5. Sıralama Ağacı (Sort Tree) Bir ikili ağaçta her kök düğümün bilgi içeriği alfabetik ve sayısal yönden sol alt ağacındaki tüm değerlerden büyük sağ alt ağacındaki tüm değerlerden küçük veya eşit ise bu ikili ağaca sıralama ağacı denir.
Örnek sıralı erişimli bir ortamdan gelen tam sayılar 47, 15, 21, 54, 51 ve 54 olan bir sıralamayı tek tek gösterimi.










Hiç yorum yok:
Yorum Gönder