Matematik ve Sayı Sistemleri Bu döküman başta olmak üzere
Matematik ve Sayı Sistemleri
Elektronik ve Sayı Sistemleri
Bilgisayar ve Sayı Sistemleri
biçiminde okunarak ilerlenmesi gerekir.
Bilgisayar ve Elektronik ile uğraşanların kesinlikle bilmesi gereken. Bilgisayarın ve elektroniğin olmazsa olmazı sayısal matematik ve sayısal elektronik.
Modern Matematik Decimal Sayı Sistemi (Onluk Taban)
Decimal sistem gündelik hayatımızda kullandığımız matematik biçimidir. Sayı tabanını 10 olarak alırız ve kullandığımız rakamlar toplam 10 tanedir. 0, 1, 2, 3, 4, 5, 6, 7, 8 ve 9. Gerçek anlamda matematik için doğal ve gerçek bir sayı sistemi ve tabanı yoktur zira matematikte tabanlarda sadece bizim rahat anlamamız için kullandığımız birimlerdir. Nasıl ki litre, kilo gibi ölçüm birimlerimiz varsa matematik içinde sayısal birimlerimiz var. Bu gerçeğe dayanarak şunu da söyleyebiliriz istediğiniz bir sayı tabanını biz kendinizde oluşturabilirsiniz. Düşününki kendi sayı sistemimizi oluşturacağız öyleyse önce bir taban belirleyelim. Tabanımız 2'nin herhangi bir katı olmalı. Buna dayanarak ta şunu söyleyebiliriz en küçük sayı sistemi tabanı 21 = 2 yani ikilik sayı sistemi. Üst sınır ise yoktur, fakat karmaşa yaratmaması için 16'lık tabandan ilerisini teoride düşlesek bile pratik ve gündelik hayatta pek göremeyiz. Standart olarak kullanılan sayı sistemleri ve isimleri
| Standart Adı | Kullanılan sayılar | |
| Binary | 21=2 İkilik Taban | 0, 1 |
| Octal | 23=8 Sekizlik Taban | 0, 1, 2, 3, 4, 5, 6, 7 |
| Decimal | Onluk Taban | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Hexdecimal | 24=16 On Altılık Taban | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Hemen aklınıza Hexdecimal için şu soru gelebilir. İyide ABCDEF bunlar rakam değil ! Evet değiller ama rakamımız bitti bizde onun için sembolik olarak rakam yerine bildik harfleri devam ettiriyoruz. Daha detaylı bilgi Hexdecimal başlığı altında bulabilirsiniz.
Binary Matemetiği (İkilik Sayı Sistemi)
Kullanılabilir en küçük sayı sistemidir. Sadece olmak yada olmamak olasılıkları vardır. Binary sistemde 1 ve 0'larla yazılamayacak sayı yoktur. Bu sayılara doğal pozitif ve negatif sayılar, ondalık içeren küsuratlı sayılarda dahil. Koordinat sistemi üzerinde gösterilebilen tüm sayılar ve reel sayılar diğer sayısal tabanlarda da gösterilebilir. İkilik sistem için kullanılan rakamlar 1 ve 0 yani var ve yok olduğu için isimleri de aynısıdır. 1=(var, SET, TRUE) ve 0=(yok, RESET, FALSE) olarak adlandırılır. Ayrıca 1 veya 0 rakamına binary sisteminde bit denilir. Bu isimler standarttır ve ilgili her yerde görürsünüz. İkilik sayı sistemindeki bir rakamı başka bir sayı sistemine çevirmeyi ve başka bir sayı sistemindeki rakamı tekrar ikilik sisteme çevirmeye bakalım.
Onluk sistemdeki bir sayıyı ikilik sisteme çevirmek
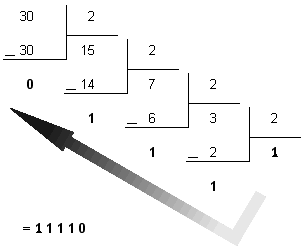
Çevirme işlemi onluk sayıyı sürekli 2'ye bölerek yapılır. Kalan 2'ye bölünemeyecek kadar küçüldüğünde tüm kalanlar (koyu rakamlar) tersten yazılır.
İkilik sistemi geri onluk sisteme çevirmek
Rakamlar ters olarak yazıldıktan sonra her rakam sıralama numarasına (n) göre 2(n) ile çarpılır ve toplamları alınır. Formülü karışık bulanlar için kendi kullandığım yöntemi de aktarmak istiyorum.
(1110)2 = ((0x20)+(1x21)+(1x22)+(1x23)+(1x24))10
(1110)2 = ((0)+(2)+(4)+(8)+(16))10
(1110)2 = (30)10

Rakamları yazdıktan sonra 1'den başlayarak 2 katlarını yazıyorum. Daha sonra karşısında 1 olanları topluyorum. Örnekte kırmızı renkte olanları toplayınca binary 5 bitlik 11110 sayılarının decimal olarak 30 olduğunu görüyoruz.
Mantık Kapıları
Standart mantık kapıları AND, OR, XOR, NOT ve türemiş halleri NAND, NOR ve NXOR'dur. Kapıları daha iyi anlatmak için AND kapısını söze dekelim. Örneğin oksijen ve lpg tanklarımız olsun. Tankımızın ateş oluşturabilmesi için her iki tüpünde içinin dolu olması gerekir yani OKSİJEN AND LPG = TRUE söylemi doğru olmalıdır. Söylemi şu şekilde kendi dilimize çevirelim EĞER OKSİJEN VE LPG VARSA TAMAM. Herhangi birisi veya her ikisi birden yoksa tabii ki sonuçta FALSE (olumsuz) olacak.
Mantık işlemlerine kapı denmesinin amacı iyi bir benzetmeden dolayıdır. Örneğin 4 kapıdan bilgiler girer ama tek kapıdan çıkar.
Şimdide türemiş kapılara bakalım
AND GATE\ (ve kapısı)
Sonuç: Yalnızca her iki tank doluysa yanma oluşabilir. | OR GATE (veya kapısı)
Sonuç: Kıvılcımın oluşması için herhangi birinin olması yeterlidir veya ikiside olabilir. | XOR GATE (özel veya kapısı)
Sonuç: Yalnızca erkek ve dişinin çocuğu olabilir :) | NOT GATE (değil kapısı)
Sonuç: FB kazanırsa; FB sevinir GS üzülür. GS kazanırsa; GS sevinir FB üzülür. |
Türemiş mantık kapıları doğal mantık kapıların birbirlerine eklenmesiyle oluşur. Doğal bir kapının önüne NOT işlemi gelince olan bu kapılar bazı durumlarda arkadaşlarını yerine geçer.
NAND (ve değil)
| NOR (veya değil)
| NXOR (özel veya değil)
|
Octal Sayı Sistemi (Sekizlik Taban)
8 rakamdan oluşan
Binary mantık kapılarının genel çalışma prensipleri böyle. Bu bilgilerin kalanı ileriki sayılarda bulacaksınız.
Octal Sayı Sistemi (Sekizlik Taban)
bu sistem çok nadir kullanılmaktadır. Genelde BCD (Binary Coded Decimal) gibi 4 bitlik data aktarımında kullanılır. Octal sistemde diğer sayı sistemlerine aynı şekilde dönüştürülür. Bu sayı sistemi üzerinde fazla durmuyorum çünkü bu sayı sistemini bilmeme rağmen hiç karşılaşmadım...
Hexdecimal Sayı Sistemi (On Altılık Taban)
16 rakamdan oluşur. 9'dan sonra rakam bittiği için 0123456789, 10=A, 11=B, 12=C, 13=D, 14=E, 15=F olarak adlandırılır. Bilgisayar veri birimleri Hexdecimal üzerine kurulmuştur. Aşağıda ki tabloda bunun katları verilmiştir. Tek bir haneden oluşan Hexdecimal sayı 1 byte eder. Hexadecimal 1 byte bilginin oluşturduğu standart veriye oktet denilir.
| Decimal Karşılığı | Adı | |
| 1 byte (1 oktet) | 0 .. 255 = 28 bit | byte, character |
| 2 byte (2 oktet veri) | 0 .. 65536 = 216 bit | word |
| 4 byte (4 oktet veri) | 0 .. 4294967296 = 232 bit | double, double word |
| 8 byte (8 oktet veri) | 0 .. 18446744073709551616 = 264 bit | long double |
Tabloda gördüğünüz rakamların hepsi pozitif ve tam sayılardı fakat bilgisayarda kullandığımız veriler hem negatif hem de küsuratlı olabilir.
| 1 byte | -128 .. 127 | short integer |
| 2 byte | -32768 .. 32767 | integer |
| 4 byte | -2147483648 .. 2147483647 | long integer |
| 4 byte | 1.5 x 10–45 .. 3.4 x 10^38 | single (7, 8 haneli) |
| 8 byte | 5.0 x 10–324 .. 1.7 x 10^308 | double (15, 16 haneli) |
| 8 byte | –922337203685477.5808 .. 922337203685477.5807 | currency (19, 20 haneli) |
Negatif olabilen sayılara işaretli sayılar denir. Bu sayıların ilk biti S (signal) yani işaret biti olarak adlandırılır. Küsuratlı sayılara ise duyarlıklı sayılar denilir. Noktadan sonra gelen kısım sayının duyarlılığını belirtir. Örneğin currency değişken tipi 4 hane duyarlıklı bir sayı tipidir.
Decimal sayı sistemini Hexdecimal sayı sistemine çevirmek
Decimal sayı yazıldıktan sonra sürekli 16'ya kadar bölünür ta ki 16'ya bölünemeyecek kadar küçük oluncaya kadar. Daha sonra çıkan sonuçlar (koyu siyah rakamlar) Eğer Hexdecimal ifade edilebilecek büyüklükteyse (10=A, 11=B, 12=C, 13=D, 14=E, 15=F) olarak adlandırılır. En son bölme işleminden itibaren her bir 2'li grup arasında yer değiştirme yapılır. Son olarak bu gruplar tersten itibaren ters olarak yazılır. Akış diyagramını yukardan aşağıya doğru işlem sırasına göre izleyebilirsiniz.
Hexdecimal sayı sistemini Decimal sayı sistemine çevirmek
Örnekte 2 byte (word) veri tipindeki bir Hexdecimal sayı Decimal sayıya dönüştürülmüştür. Bu işlem yapılırken de önce sayılar byte biçiminde tersten yazılırlar. Örnekte de görebileceğiniz gibi EF10 terse çevrilirken EF'10 biçimiyle ters çevrilir. Yani 10'FE olarak byte byte ters çevrilir. Ayrıca bu ters yapı dosyaların içine gömülü sayı değerleri içinde kullanılır.
(EF10)16 = ((1x160)+(0x161)+(Fx162)+(Ex163))10
(EF10)16 = ((1)+(0)+(3840)+(57344))10
(EF10)16 = (61200)10
Hexdecimal sayı sistemini diğer sayı sistemlerine çevirirken
Hexdecimal bir sayısı binary sayıya yine 2'ye bölme metodunu kullanarak yapabilirsiniz zorlanırsanız önce Decimal'e sonra yine Binary'e çevirme işlemide bir çözüm tabii. Unutmamanız gereken A'yı tek başına 10 gibi düşünmenizdir. Yoksa sonuç hatası yaparsınız.
Not: Bu yazıyla ilgili görüşleriniz için

Hiç yorum yok:
Yorum Gönder